 View on QuantumAI View on QuantumAI
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
|
try:
import cirq
except ImportError:
print("installing cirq...")
!pip install --quiet cirq
print("installed cirq.")
import cirq
A Gate is an effect that can be applied to a collection of
qubits (objects with a Qid). Gates can be applied
to qubits by calling their on method, or, alternatively
calling the gate on the qubits. The object created by such calls
is an Operation. Alternatively, a Gate can be thought of
as a factory
that, given input qubits, generates an associated
GateOperation object.
Gates versus operations
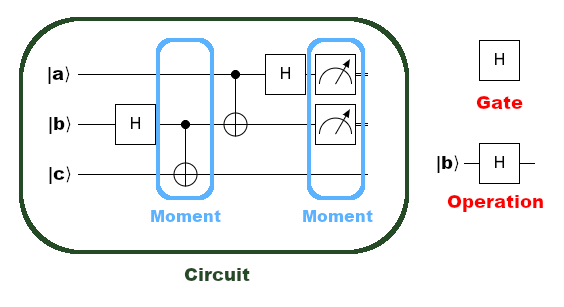
The above example shows the first half of a quantum teleportation circuit,
found in many quantum computation textbooks. This example uses three different
gates: a Hadamard (H), controlled-Not (CNOT), and measurement. These are
represented in cirq by cirq.H, cirq.CNOT, and cirq.measure,
respectively.
In this example, a Hadamard is an example of a Gate object that can be applied
in many different circumstances and to many different qubits. Note that the
above example has two instances of an H gate but applied to different qubits.
This is an example of one Gate type with two Operation instances, one
applied to the qubit '|b⟩' and the other applied to qubit '|a⟩'.
Gates can generally be applied to any type of qubit (NamedQubit,
LineQubit, GridQubit, etc. - see Qubits for more details) to create an Operation.
The following example shows how to construct each of these gates and operations.
# This examples uses named qubits to remain abstract.
# However, we can also use LineQubits or GridQubits to specify a geometry
a = cirq.NamedQubit('a')
b = cirq.NamedQubit('b')
c = cirq.NamedQubit('c')
# Example Operations, that correspond to the moments above
print(cirq.H(b))
print(cirq.CNOT(b, c))
print(cirq.CNOT(a, b))
print(cirq.H(a))
print(cirq.measure(a, b))
H(b) CNOT(b, c) CNOT(a, b) H(a) cirq.MeasurementGate(2, cirq.MeasurementKey(name='a,b'), ())(a, b)
This would create the operations needed to comprise the circuit from the above diagram. The next step would be composing these operations into moments and circuits. For more on those types, see the documentation on Circuits.
Immutability of Gates and Operations
Gates and Operations in Cirq are considered to be immutable objects. This means that a cirq.Gate or cirq.Operation should not be modified after its creation. If attributes of these objects need to be modified, a new object should be created.
Modifying these objects in-place could cause unexpected behavior. For instance, changing the qubits of an existing cirq.Operation object could cause an existing cirq.Moment that contains this object to have operations with overlapping qubits.
Other gate features
Most Gates operate on a specific number of qubits, which can be accessed
by the num_qubits() function. One notable exception is the
MeasurementGate which can be applied to a variable number of qubits.
Most gates also have a unitary matrix representation, which can be accessed
by cirq.unitary(gate).
Not all Gates correspond to unitary evolution. They may represent a
probabilistic mixture of unitaries, or a general quantum channel. The component
unitaries and associated probabilities of a mixture can be accessed by
cirq.mixture(gate). The Kraus operator representation of a channel can be
accessed by cirq.kraus(gate). Non-unitary gates are often used in the
simulation of noise. See noise documentation for more details.
Many arithmetic operators will work in the expected way when applied to
gates. For instance, cirq.X**0.5 represents a square root of X gate.
These can also be applied to Operators for a more compact representation, such
as cirq.X(q1)**0.5 will be a square root of X gate applied to the q1
qubit. This functionality depends on the "magic methods" of the gate
being defined (see below for details).
Gates can be converted to a controlled version by using Gate.controlled().
In general, this returns an instance of a ControlledGate. However, for
certain special cases where the controlled version of the gate is also a
known gate, this returns the instance of that gate.
For instance, cirq.X.controlled() returns a cirq.CNOT gate.
Operations have similar functionality Operation.controlled_by(), such as
cirq.X(q0).controlled_by(q1).
Common gates
Cirq supports a number of gates natively, with the opportunity to extend these gates for more advanced use cases.
Measurement gate
cirq.MeasurementGate This is a measurement in the computational basis.
This gate can be applied to a variable number of qubits. The function
cirq.measure(q0, q1, ...) can also be used as a short-hand to create a
MeasurementGate .
Single qubit gates
Most single-qubit gates can be thought of as rotation around an axis in the Bloch Sphere representation and are usually referred to by their axis of rotation. Some operators use the notation of a 'half-turn' which is defined as a 180 degree (pi radians) rotation around the axis.
cirq.X / cirq.Y / cirq.Z The Pauli gates X, Y, and Z which rotate the state around the associated axis by one half-turn.
cirq.rx(rads) A rotation about the Pauli 'X' axis in terms of radians. This is equivalent to exp(-i X rads / 2) = cos(rads/2) I - i sin(rads/2) X
cirq.ry(rads) A rotation about the Pauli 'Y' axis in terms of radians. This is equivalent to exp(-i Y rads / 2) = cos(rads/2) I - i sin(rads/2) Y
cirq.rz(rads) A rotation about the Pauli 'Z' axis in terms of radians. This is equivalent to exp(-i Z rads / 2) = cos(rads/2) I - i sin(rads/2) Z
cirq.XPowGate(exponent=t) Rotations about the Pauli X axis, equivalent to cirq.X**t. See cirq.XPowGate for its unitary matrix. Note that this has a global phase of e^{i·π·t/2} versus the traditionally defined rotation matrix, which can be modified by the optional parameter global_shift.
cirq.YPowGate(exponent=t) Rotations about the Pauli Y axis, equivalent to cirq.Y**t. See cirq.YPowGate for its unitary matrix. Note that this has a global phase of e^{i·π·t/2} versus the traditionally defined rotation matrix, which can be modified by the optional parameter global_shift.
cirq.ZPowGate(exponent=t) Rotations about the Pauli Z axis, equivalent to cirq.Z**t. See cirq.ZPowGate for its unitary matrix. Note that this has a global phase of e^{i·π·t/2} versus the traditionally defined rotation matrix, which can be modified by the optional parameter global_shift.
cirq.PhasedXPowGate
This gate is a rotation about an axis in the XY plane of the Bloch sphere.
The PhasedXPowGate takes two parameters, exponent and phase_exponent.
The gate is equivalent to the circuit ───Z^-p───X^t───Z^p─── where p is the
phase_exponent and t is the exponent.
cirq.PhasedXZGate
This gate is like a cirq.PhasedXPowGate above, but it also includes an
extra phase about the z axis. PhasedXZGate takes three parameters, x_exponent, z_exponent, and axis_phase_exponent. The gate is equivalent to the circuit ───Z^(-a)──X^x──Z^a────Z^z─── where x is the x_exponent, z is the z_exponent, and a is the axis_phase_exponent.
cirq.H / cirq.HPowGate The Hadamard gate is a rotation around the X+Z axis.
cirq.HPowGate(exponent=t) is a variable rotation of t turns around this
axis. cirq.H is a π rotation and is equivalent to
cirq.HPowGate(exponent=1)
S The square root of Z gate, equivalent to cirq.Z**0.5
T The fourth root of Z gate, equivalent to cirq.Z**0.25.
Two qubit gates
cirq.CZ / cirq.CZPowGate The controlled-Z gate. A two qubit gate that
phases the |11⟩ state. cirq.CZPowGate(exponent=t) is equivalent to
cirq.CZ**t and has a matrix representation of exp(i pi |11⟩⟨11| t).
cirq.CNOT / cirq.CNotPowGate The controlled-X gate. This gate swaps the
|11⟩ and |10⟩ states. cirq.CNotPowGate(exponent=t) is equivalent
to cirq.CNOT**t .
cirq.SWAP / cirq.SwapPowGate The swap gate swaps the |01⟩ and |10⟩ states.
cirq.SWAP**t is the same as cirq.SwapPowGate(exponent = t)
cirq.ISWAP / cirq.ISwapPowGate The iSwap gate swaps the |01⟩ and |10⟩
states and adds a relative phase of i. cirq.ISWAP**t is the same as
cirq.ISwapPowGate(exponent = t)
Parity gates: The gates cirq.XX, cirq.YY, and cirq.ZZ are equivalent to
performing the equivalent one-qubit Pauli gates on both qubits. The gates
cirq.XXPowGate, cirq.YYPowGate, and cirq.ZZPowGate are the powers of
these gates.
Other gates
cirq.MatrixGate: A gate defined by its unitary matrix in the form of a numpy ndarray.
cirq.WaitGate: This gate does nothing for a specified cirq.Duration
amount of time. This is useful for conducting T1 and T2 decay experiments.
cirq.CCNOT, cirq.CCX, cirq.TOFFOLI, cirq.CCXPowGate: Three qubit gates representing a controlled-controlled-X gate and powers of this gate.
cirq.CCZ, cirq.CCZPowGate: Three qubit gates representing a controlled-controlled-Z gate and power of this gate.
CSWAP, CSwapGate, FREDKIN: Three qubit gates representing a controlled-SWAP gate.
TwoQubitDiagonalGate, ThreeQubitDiagonalGate: Two and three qubit gates which are diagonal in the computational basis.
QubitPermutationGate A gate that permutes a given set of qubits.
Advanced: create your own gates
If the above gates are not sufficient for your use case, it is fairly simple
to create your own gate. In order to do so, you can define your class and
inherit the cirq.Gate class and define the functionality in your class.
For more information, see this guide.
