 View on QuantumAI View on QuantumAI
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
|
try:
import cirq
except ImportError:
print("installing cirq...")
!pip install --quiet cirq
print("installed cirq.")
import cirq
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
TiltedSquareLattice
This is a grid lattice rotated 45-degrees.
This topology is based on Google devices where plaquettes consist of four qubits in a square connected to a central qubit:
x x
x
x x
import itertools
from cirq import TiltedSquareLattice
side_lens = np.arange(1, 4 + 1)
l = len(side_lens)
fig, axes = plt.subplots(l, l, figsize=(3.5 * l, 3 * l))
for widthi, heighti in itertools.product(np.arange(l), repeat=2):
width = side_lens[widthi]
height = side_lens[heighti]
ax = axes[heighti, widthi]
topo = TiltedSquareLattice(width, height)
topo.draw(ax=ax, tilted=False)
if widthi == 0:
ax.set_ylabel(f'Height {height}', fontsize=14)
if heighti == l - 1:
ax.set_xlabel(f'Width {width}', fontsize=14)
ax.set_title(f'n = {topo.n_nodes}', fontsize=14)
fig.tight_layout()
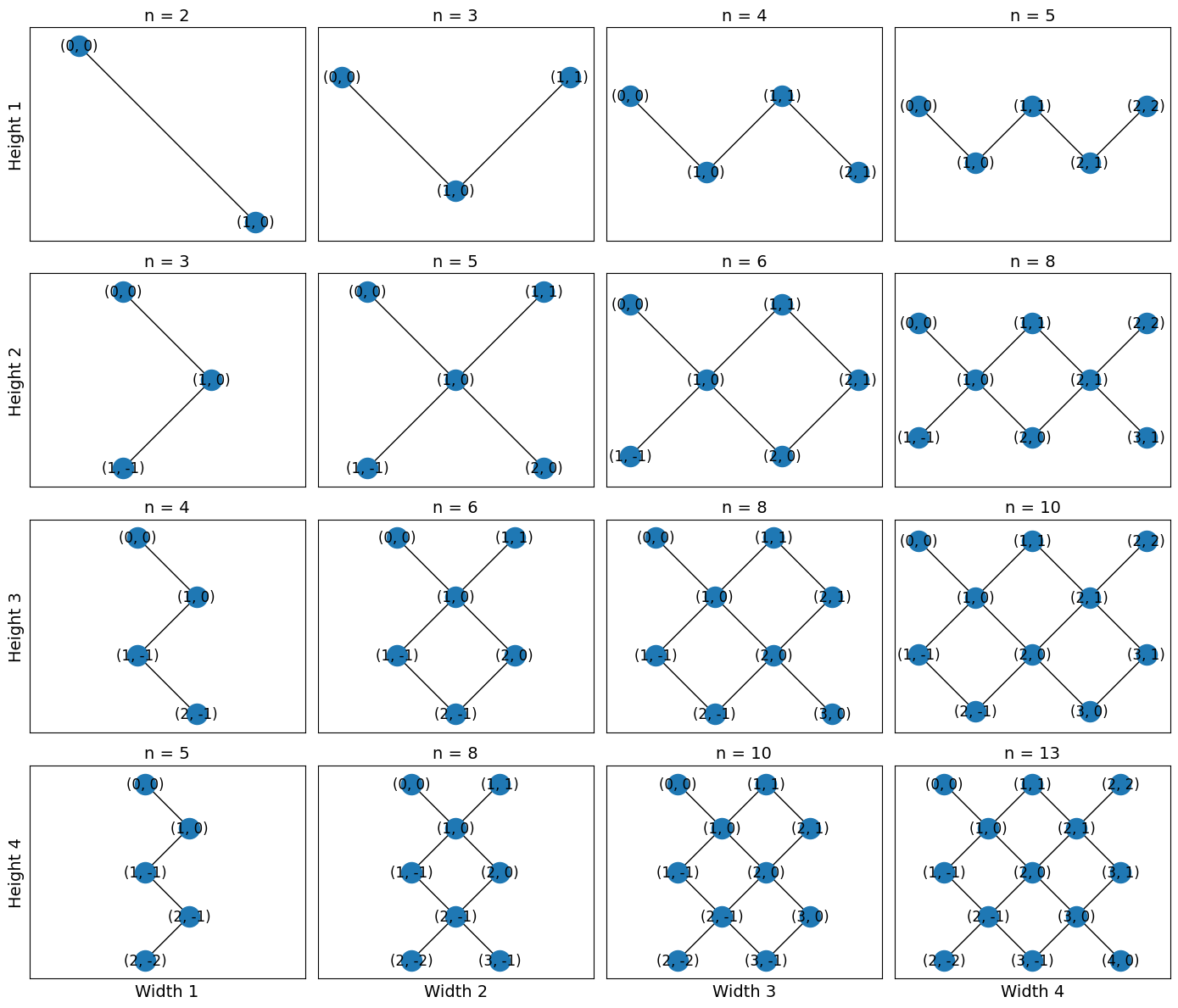
The corner nodes are not connected to each other. width and height refer to the rectangle
formed by rotating the lattice 45 degrees. width and height are measured in half-unit
cells, or equivalently half the number of central nodes.
Nodes are 2-tuples of integers which may be negative. Please see get_placements for
mapping this topology to a GridQubit Device.
Placement
import networkx as nx
SYC23_GRAPH = nx.from_edgelist(
[
((3, 2), (4, 2)),
((4, 1), (5, 1)),
((4, 2), (4, 1)),
((4, 2), (4, 3)),
((4, 2), (5, 2)),
((4, 3), (5, 3)),
((5, 1), (5, 0)),
((5, 1), (5, 2)),
((5, 1), (6, 1)),
((5, 2), (5, 3)),
((5, 2), (6, 2)),
((5, 3), (5, 4)),
((5, 3), (6, 3)),
((5, 4), (6, 4)),
((6, 1), (6, 2)),
((6, 2), (6, 3)),
((6, 2), (7, 2)),
((6, 3), (6, 4)),
((6, 3), (7, 3)),
((6, 4), (6, 5)),
((6, 4), (7, 4)),
((6, 5), (7, 5)),
((7, 2), (7, 3)),
((7, 3), (7, 4)),
((7, 3), (8, 3)),
((7, 4), (7, 5)),
((7, 4), (8, 4)),
((7, 5), (7, 6)),
((7, 5), (8, 5)),
((8, 3), (8, 4)),
((8, 4), (8, 5)),
((8, 4), (9, 4)),
]
)
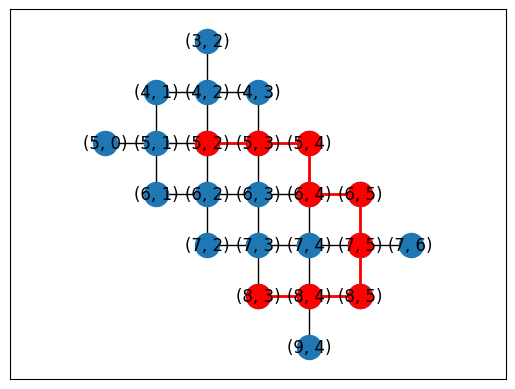
You can manually generate mappings between NamedTopology nodes and device qubits using helper functions.
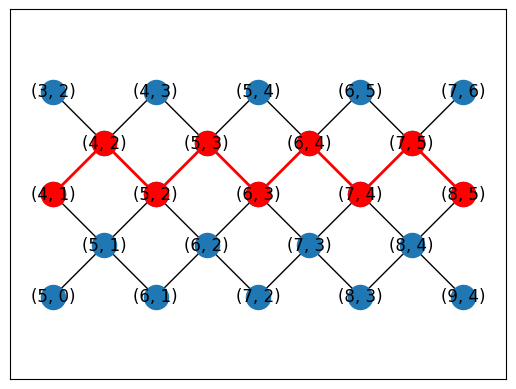
topo = TiltedSquareLattice(4, 2)
cirq.draw_placements(
SYC23_GRAPH,
topo.graph,
[topo.nodes_to_gridqubits(offset=(3, 2)), topo.nodes_to_gridqubits(offset=(5, 3))],
tilted=False,
)
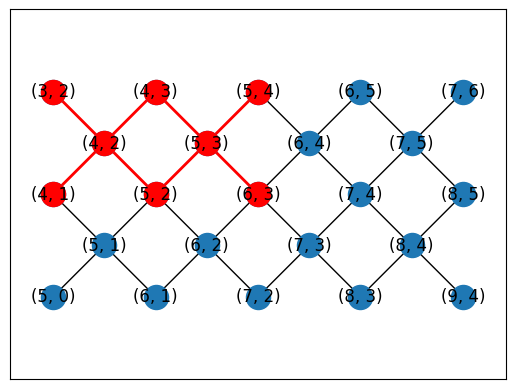
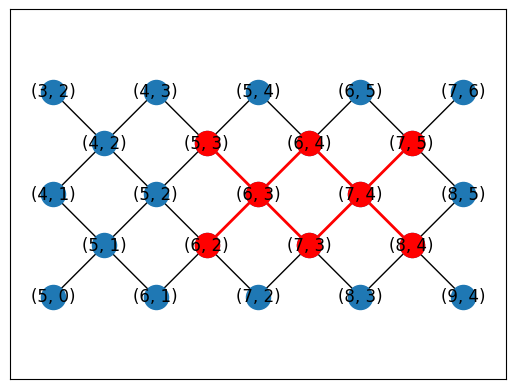
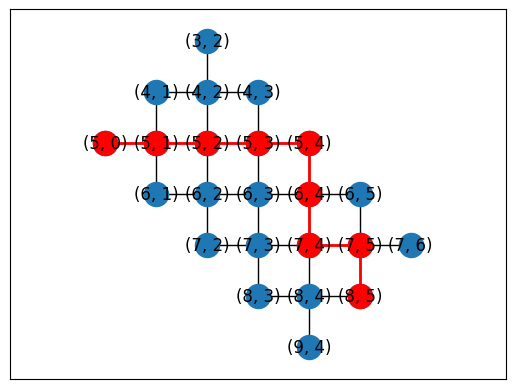
Or you can automatically generate placements using a subgraph monomorphism algorithm in NetworkX.
topo = TiltedSquareLattice(4, 2)
placements = cirq.get_placements(SYC23_GRAPH, topo.graph)
cirq.draw_placements(SYC23_GRAPH, topo.graph, placements[::3])
print('...\n')
print(f'{len(placements)} total placements')
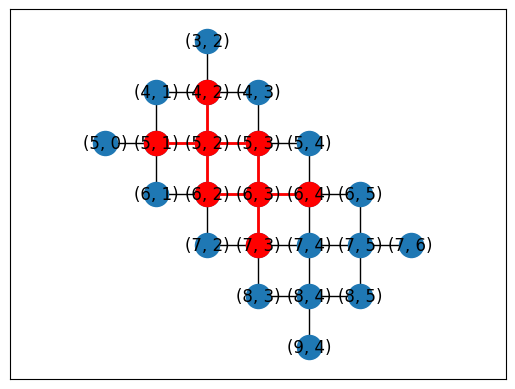
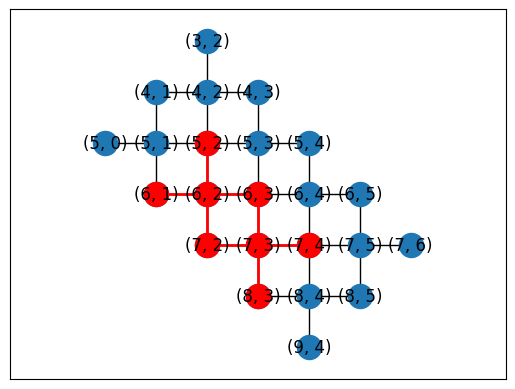
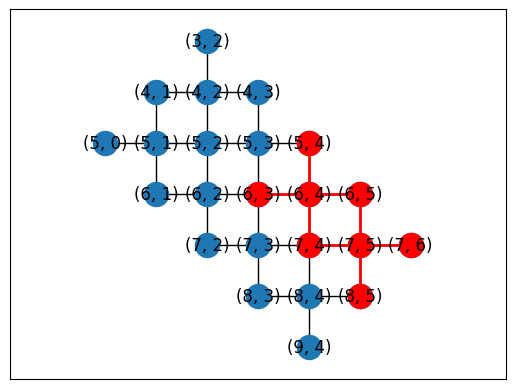
... 12 total placements
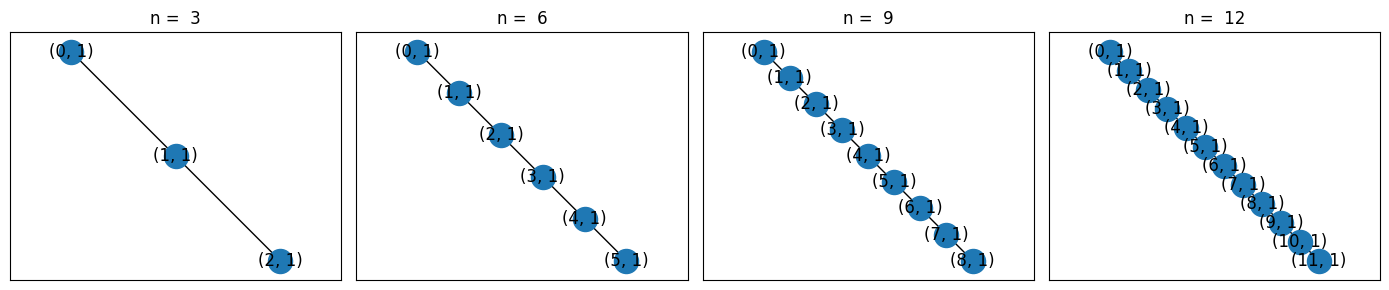
LineTopology
This is a 1D linear topology.
Node indices are contiguous integers starting from 0 with edges between adjacent integers.
from cirq import LineTopology
lens = np.arange(3, 12 + 1, 3)
l = len(lens)
fig, axes = plt.subplots(1, l, figsize=(3.5 * l, 3 * 1))
for ax, n_nodes in zip(axes, lens):
LineTopology(n_nodes).draw(ax=ax, tilted=False)
ax.set_title(f'n = {n_nodes}')
fig.tight_layout()
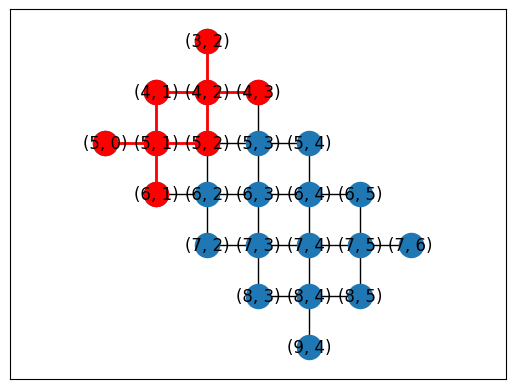
Manual placement
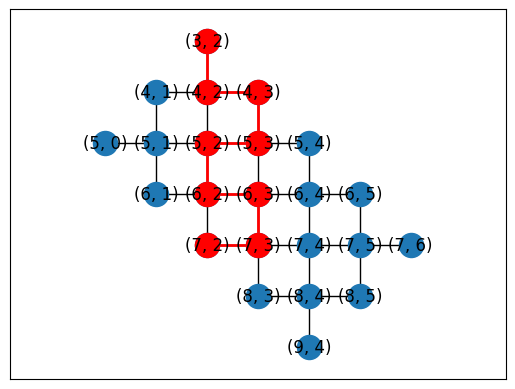
topo = LineTopology(9)
cirq.draw_placements(
SYC23_GRAPH,
topo.graph,
[
{
i: q
for i, q in enumerate(
[
cirq.GridQubit(4, 1),
cirq.GridQubit(4, 2),
cirq.GridQubit(5, 2),
cirq.GridQubit(5, 3),
cirq.GridQubit(6, 3),
cirq.GridQubit(6, 4),
cirq.GridQubit(7, 4),
cirq.GridQubit(7, 5),
cirq.GridQubit(8, 5),
]
)
}
],
tilted=False,
)
Automatic placement
topo = LineTopology(9)
placements = cirq.get_placements(SYC23_GRAPH, topo.graph)
cirq.draw_placements(SYC23_GRAPH, topo.graph, placements[::300])
print('...\n')
print(f'{len(placements)} total placements')
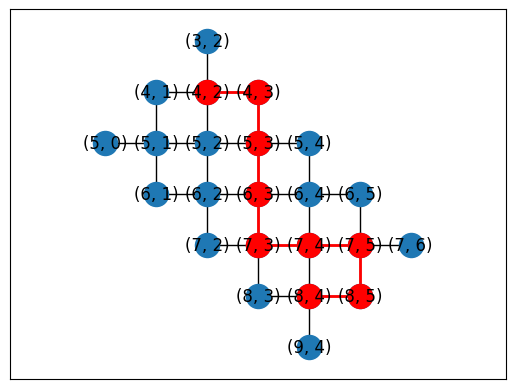
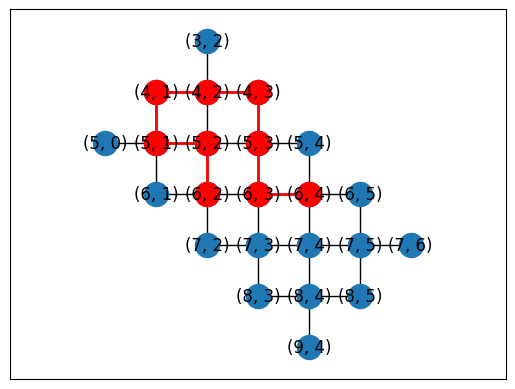
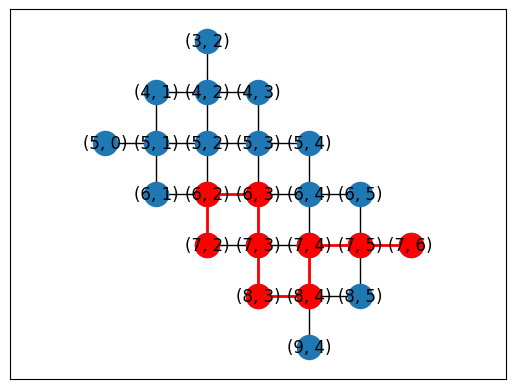
... 1615 total placements
