Named Topologies

try:
    import cirq
except ImportError:
    print("installing cirq...")
    !pip install --quiet cirq
    print("installed cirq.")

import cirq

import matplotlib.pyplot as plt
import numpy as np
import networkx as nx

TiltedSquareLattice

This is a grid lattice rotated 45-degrees.

This topology is based on Google devices where plaquettes consist of four qubits in a square connected to a central qubit:

x   x
  x
x   x

import itertools
from cirq import TiltedSquareLattice

side_lens = np.arange(1, 4 + 1)
l = len(side_lens)

fig, axes = plt.subplots(l, l, figsize=(3.5 * l, 3 * l))
for widthi, heighti in itertools.product(np.arange(l), repeat=2):
    width = side_lens[widthi]
    height = side_lens[heighti]
    ax = axes[heighti, widthi]
    topo = TiltedSquareLattice(width, height)
    topo.draw(ax=ax, tilted=False)

    if widthi == 0:
        ax.set_ylabel(f'Height {height}', fontsize=14)
    if heighti == l - 1:
        ax.set_xlabel(f'Width {width}', fontsize=14)

    ax.set_title(f'n = {topo.n_nodes}', fontsize=14)

fig.tight_layout()

png

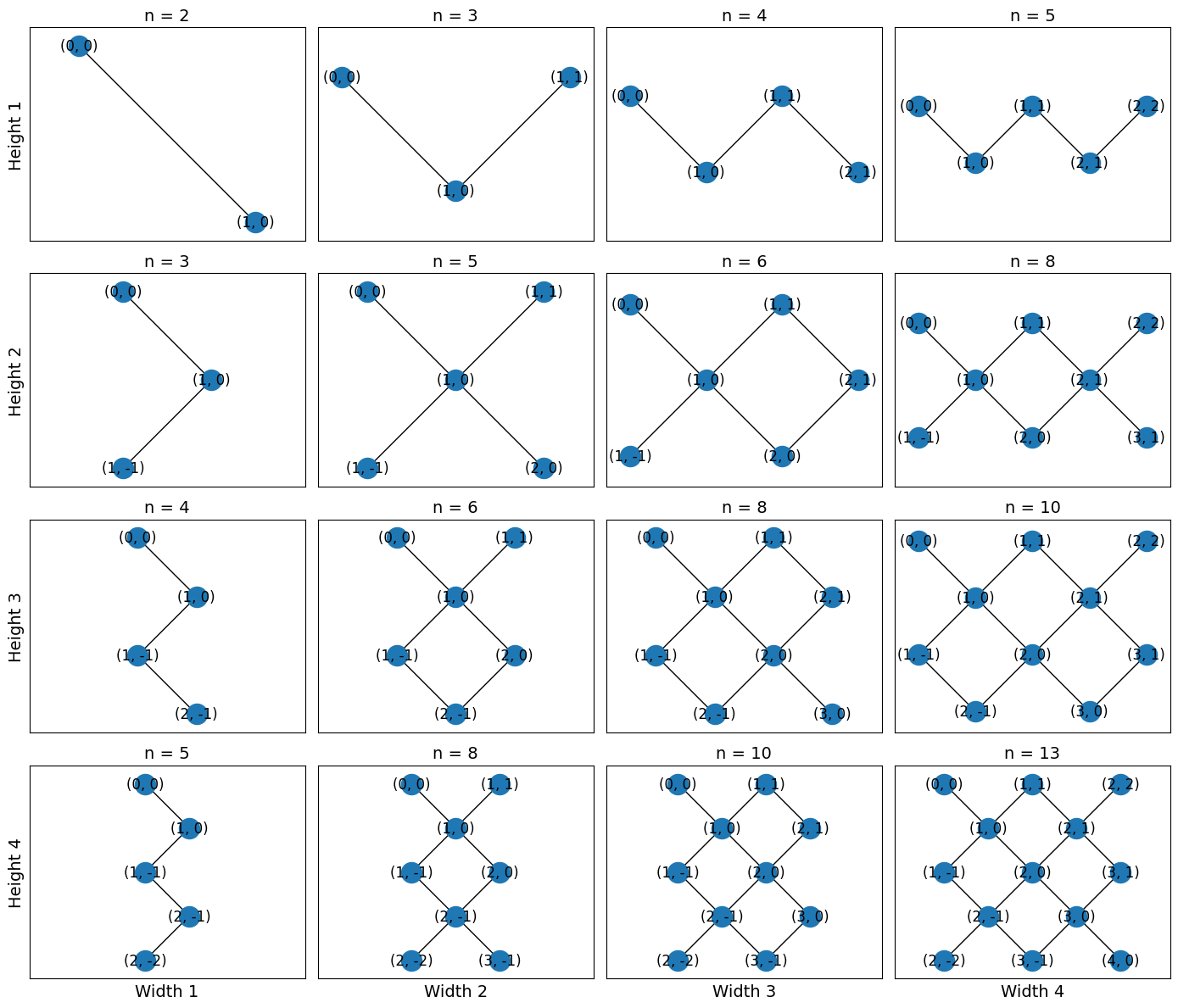
The corner nodes are not connected to each other. width and height refer to the rectangle formed by rotating the lattice 45 degrees. width and height are measured in half-unit cells, or equivalently half the number of central nodes.

Nodes are 2-tuples of integers which may be negative. Please see get_placements for mapping this topology to a GridQubit Device.

Placement

import networkx as nx

SYC23_GRAPH = nx.from_edgelist(
    [
        ((3, 2), (4, 2)),
        ((4, 1), (5, 1)),
        ((4, 2), (4, 1)),
        ((4, 2), (4, 3)),
        ((4, 2), (5, 2)),
        ((4, 3), (5, 3)),
        ((5, 1), (5, 0)),
        ((5, 1), (5, 2)),
        ((5, 1), (6, 1)),
        ((5, 2), (5, 3)),
        ((5, 2), (6, 2)),
        ((5, 3), (5, 4)),
        ((5, 3), (6, 3)),
        ((5, 4), (6, 4)),
        ((6, 1), (6, 2)),
        ((6, 2), (6, 3)),
        ((6, 2), (7, 2)),
        ((6, 3), (6, 4)),
        ((6, 3), (7, 3)),
        ((6, 4), (6, 5)),
        ((6, 4), (7, 4)),
        ((6, 5), (7, 5)),
        ((7, 2), (7, 3)),
        ((7, 3), (7, 4)),
        ((7, 3), (8, 3)),
        ((7, 4), (7, 5)),
        ((7, 4), (8, 4)),
        ((7, 5), (7, 6)),
        ((7, 5), (8, 5)),
        ((8, 3), (8, 4)),
        ((8, 4), (8, 5)),
        ((8, 4), (9, 4)),
    ]
)

You can manually generate mappings between NamedTopology nodes and device qubits using helper functions.

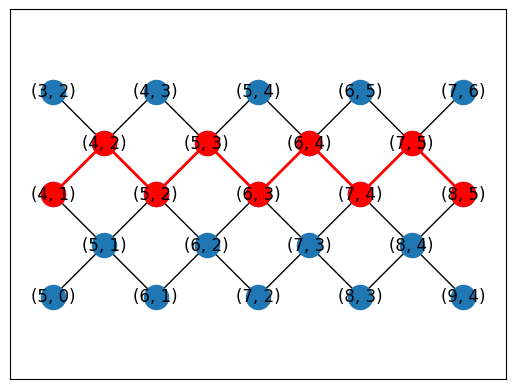
topo = TiltedSquareLattice(4, 2)

cirq.draw_placements(
    SYC23_GRAPH,
    topo.graph,
    [topo.nodes_to_gridqubits(offset=(3, 2)), topo.nodes_to_gridqubits(offset=(5, 3))],
    tilted=False,
)

png

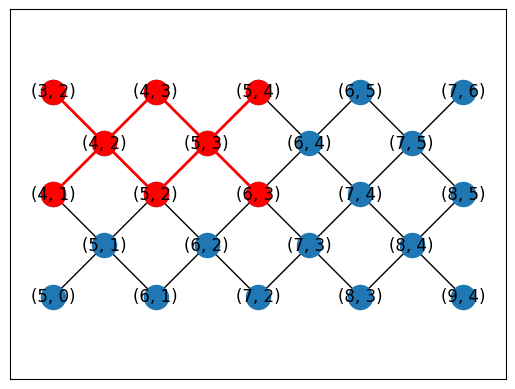
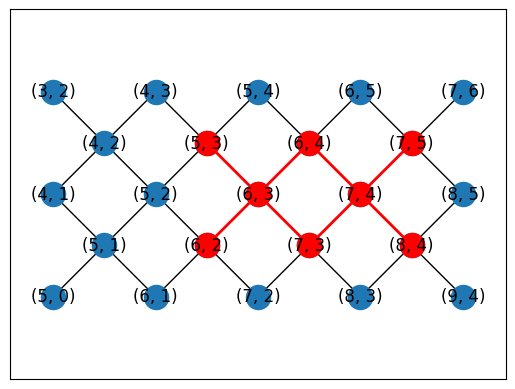
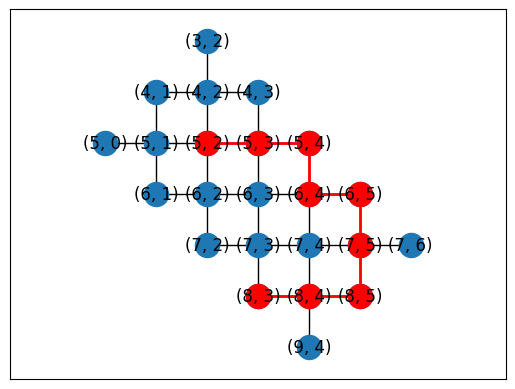
Or you can automatically generate placements using a subgraph monomorphism algorithm in NetworkX.

topo = TiltedSquareLattice(4, 2)
placements = cirq.get_placements(SYC23_GRAPH, topo.graph)
cirq.draw_placements(SYC23_GRAPH, topo.graph, placements[::3])
print('...\n')
print(f'{len(placements)} total placements')

png

...

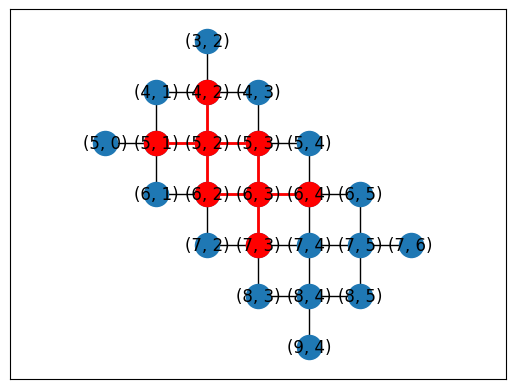
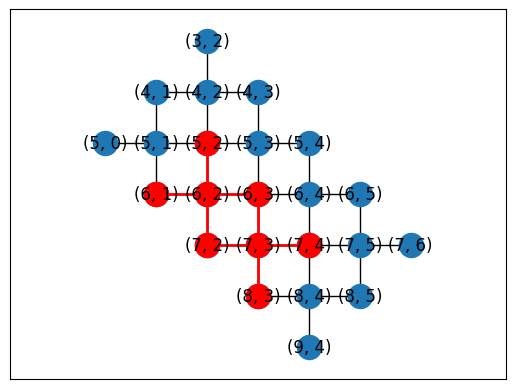
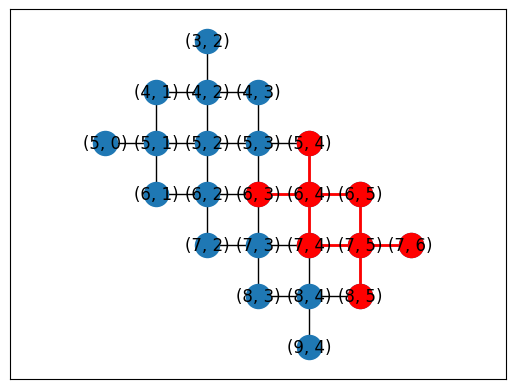
12 total placements

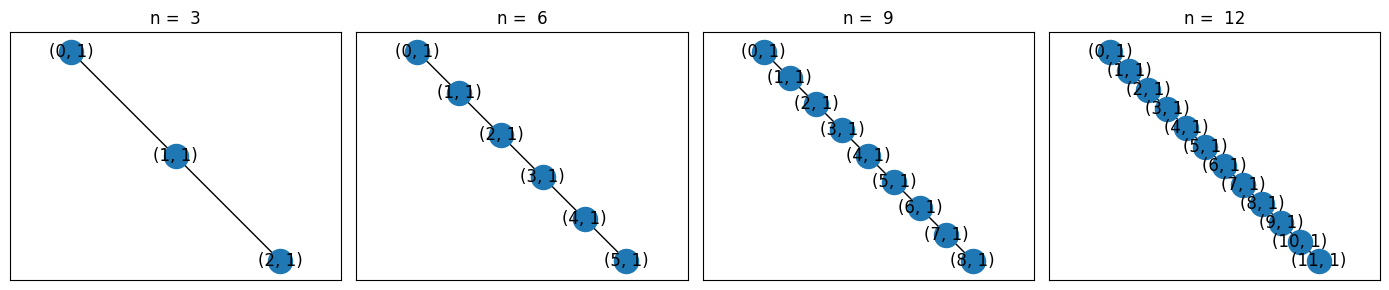
LineTopology

This is a 1D linear topology.

Node indices are contiguous integers starting from 0 with edges between adjacent integers.

from cirq import LineTopology

lens = np.arange(3, 12 + 1, 3)
l = len(lens)
fig, axes = plt.subplots(1, l, figsize=(3.5 * l, 3 * 1))

for ax, n_nodes in zip(axes, lens):
    LineTopology(n_nodes).draw(ax=ax, tilted=False)
    ax.set_title(f'n =  {n_nodes}')

fig.tight_layout()

png

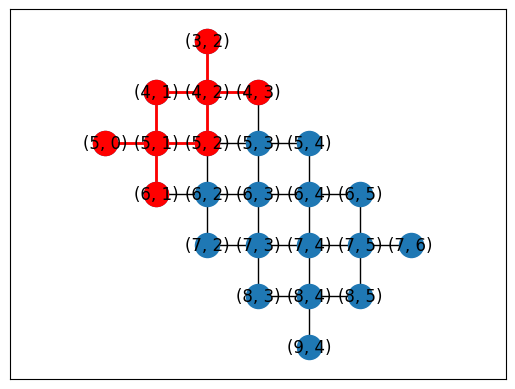
Manual placement

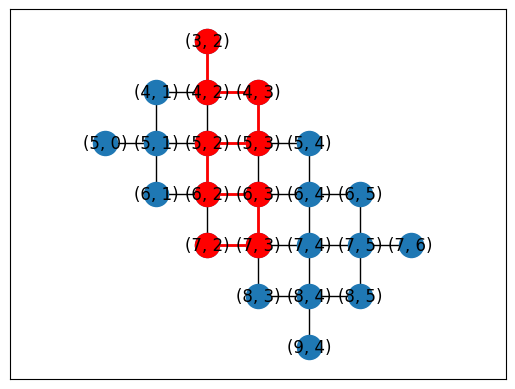
topo = LineTopology(9)

cirq.draw_placements(
    SYC23_GRAPH,
    topo.graph,
    [
        {
            i: q
            for i, q in enumerate(
                [
                    cirq.GridQubit(4, 1),
                    cirq.GridQubit(4, 2),
                    cirq.GridQubit(5, 2),
                    cirq.GridQubit(5, 3),
                    cirq.GridQubit(6, 3),
                    cirq.GridQubit(6, 4),
                    cirq.GridQubit(7, 4),
                    cirq.GridQubit(7, 5),
                    cirq.GridQubit(8, 5),
                ]
            )
        }
    ],
    tilted=False,
)

png

Automatic placement

topo = LineTopology(9)
placements = cirq.get_placements(SYC23_GRAPH, topo.graph)
cirq.draw_placements(SYC23_GRAPH, topo.graph, placements[::300])
print('...\n')
print(f'{len(placements)} total placements')

png

...

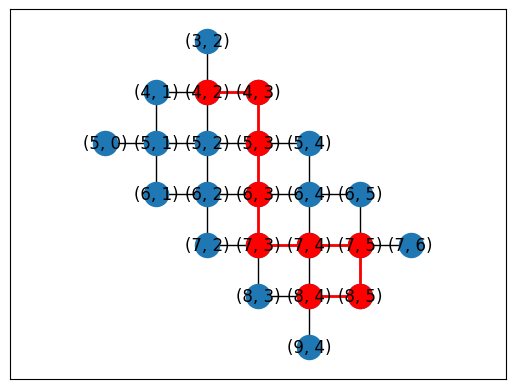
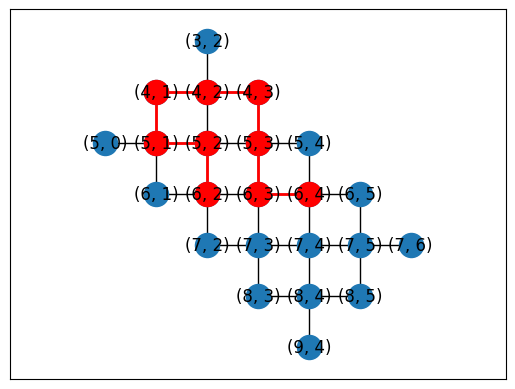
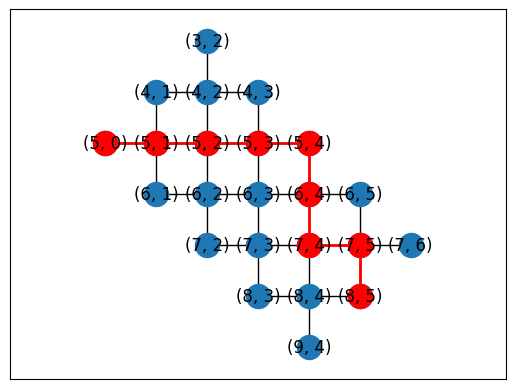
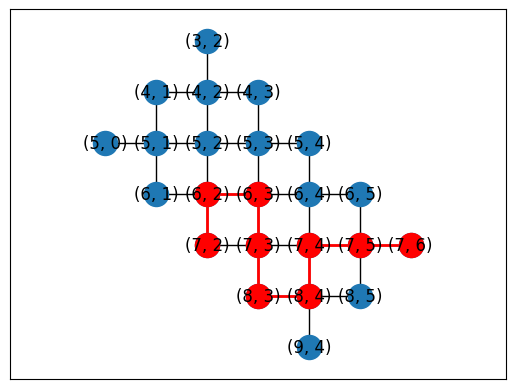
1615 total placements