This code tutorial shows how to estimate a 1-RDM and perform variational optimization
 View on QuantumAI View on QuantumAI
|
 Run in Google Colab Run in Google Colab
|
 View source on GitHub View source on GitHub
|
|
try:
import recirq
except ImportError:
!pip install --quiet git+https://github.com/quantumlib/ReCirq
import numpy as np
import cirq
from recirq.hfvqe.gradient_hf import rhf_func_generator
from recirq.hfvqe.opdm_functionals import OpdmFunctional
from recirq.hfvqe.analysis import (
compute_opdm, mcweeny_purification,
resample_opdm, fidelity_witness,
fidelity)
from recirq.hfvqe.third_party.higham import fixed_trace_positive_projection
from recirq.hfvqe.molecular_example import make_h6_1_3
Set up the experiment
Generate the input files, set up quantum resources, and set up the OpdmFunctional to make measurements.
rhf_objective, molecule, parameters, obi, tbi = make_h6_1_3()
ansatz, energy, gradient = rhf_func_generator(rhf_objective)
# settings for quantum resources
qubits = [cirq.GridQubit(0, x) for x in range(molecule.n_orbitals)]
sampler = cirq.Simulator(dtype=np.complex128) # this can be a QuantumEngine
# OpdmFunctional contains an interface for running experiments
opdm_func = OpdmFunctional(qubits=qubits,
sampler=sampler,
constant=molecule.nuclear_repulsion,
one_body_integrals=obi,
two_body_integrals=tbi,
# only simulate spin-up electrons:
num_electrons=molecule.n_electrons // 2,
clean_xxyy=True,
purification=True
)
Optimization terminated successfully.
Current function value: -2.924060
Iterations: 7
Function evaluations: 15
Gradient evaluations: 15
The displayed text is the output of the gradient based restricted Hartree-Fock. We define the gradient in rhf_objective and use the conjugate-gradient optimizer to optimize the basis rotation parameters. This is equivalent to doing Hartree-Fock theory from the canonical transformation perspective.
Estimate Quantities
Next, we will do the following:
Do measurements for a given set of parameters
Compute 1-RDM, variances, and purification
Compute energy, fidelities, and errorbars
# 1.
# default to 250_000 shots for each circuit.
# 7 circuits total, printed for your viewing pleasure
# return value is a dictionary with circuit results for each permutation
measurement_data = opdm_func.calculate_data(parameters)
# 2.
opdm, var_dict = compute_opdm(measurement_data, return_variance=True)
opdm_pure = mcweeny_purification(opdm)
# 3.
raw_energies = []
raw_fidelity_witness = []
purified_eneriges = []
purified_fidelity_witness = []
purified_fidelity = []
true_unitary = ansatz(parameters)
nocc = molecule.n_electrons // 2
nvirt = molecule.n_orbitals - nocc
initial_fock_state = [1] * nocc + [0] * nvirt
# 1000 repetitions of the measurement
for _ in range(1000):
new_opdm = resample_opdm(opdm, var_dict)
raw_energies.append(opdm_func.energy_from_opdm(new_opdm))
raw_fidelity_witness.append(
fidelity_witness(target_unitary=true_unitary,
omega=initial_fock_state,
measured_opdm=new_opdm)
)
# fix positivity and trace of sampled 1-RDM if strictly outside
# feasible set
w, v = np.linalg.eigh(new_opdm)
if len(np.where(w < 0)[0]) > 0:
new_opdm = fixed_trace_positive_projection(new_opdm, nocc)
new_opdm_pure = mcweeny_purification(new_opdm)
purified_eneriges.append(opdm_func.energy_from_opdm(new_opdm_pure))
purified_fidelity_witness.append(
fidelity_witness(target_unitary=true_unitary,
omega=initial_fock_state,
measured_opdm=new_opdm_pure)
)
purified_fidelity.append(
fidelity(target_unitary=true_unitary,
measured_opdm=new_opdm_pure)
)
print("Canonical Hartree-Fock energy ", molecule.hf_energy)
print("True energy ", energy(parameters))
print("Raw energy ", opdm_func.energy_from_opdm(opdm),
"+- ", np.std(raw_energies))
print("Raw fidelity witness ", np.mean(raw_fidelity_witness).real,
"+- ", np.std(raw_fidelity_witness))
print("purified energy ", opdm_func.energy_from_opdm(opdm_pure),
"+- ", np.std(purified_eneriges))
print("Purified fidelity witness ", np.mean(purified_fidelity_witness).real,
"+- ", np.std(purified_fidelity_witness))
print("Purified fidelity ", np.mean(purified_fidelity).real,
"+- ", np.std(purified_fidelity))
Canonical Hartree-Fock energy -2.9240604849733085 True energy -2.9240604849722285 Raw energy -2.924628569612709 +- 0.0015281717499051539 Raw fidelity witness 1.0005491174862855 +- 0.002055663647689664 purified energy -2.9240548794725822 +- 6.205204601718123e-06 Purified fidelity witness 0.9999800456287192 +- 8.57644853398966e-06 Purified fidelity 0.9999900232376692 +- 4.288132630513111e-06
This prints out the various energies estimated from the 1-RDM along with error bars. Generated from resampling the 1-RDM based on the estimated covariance.
Optimization
We use the sampling functionality to variationally relax the parameters of my ansatz such that the energy is decreased.
For this we will need the augmented Hessian optimizer
The optimizerer code we have takes: rhf_objective object, initial parameters, a function that takes a n x n unitary and returns an opdm maximum iterations, hassian_update which indicates how much of the hessian to use rtol which is the gradient stopping condition.
A natural thing that we will want to save is the variance dictionary of the non-purified 1-RDM. This is accomplished by wrapping the 1-RDM estimation code in another object that keeps track of the variance dictionaries.
from recirq.hfvqe.mfopt import moving_frame_augmented_hessian_optimizer
from recirq.hfvqe.opdm_functionals import RDMGenerator
rdm_generator = RDMGenerator(opdm_func, purification=True)
opdm_generator = rdm_generator.opdm_generator
result = moving_frame_augmented_hessian_optimizer(
rhf_objective=rhf_objective,
initial_parameters=parameters + 1.0E-1,
opdm_aa_measurement_func=opdm_generator,
verbose=True, delta=0.03,
max_iter=20,
hessian_update='diagonal',
rtol=0.50E-2)
ITERATION NUMBER : 0 unitary [[1. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0.] [0. 0. 1. 0. 0. 0.] [0. 0. 0. 1. 0. 0.] [0. 0. 0. 0. 1. 0.] [0. 0. 0. 0. 0. 1.]] Current Energy: -2.8260574261566243 true energy -2.8262712927716622 dvec [(np.complex128(0.12544149900017482+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.1488432401199553+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.109457750436557+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.3326789670633076+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.14291055778220318+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.2649553873783967+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.2082761858669262+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.22071570098343762+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.2361989769388798+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.05231051648282431 ITERATION NUMBER : 1 unitary [[ 0.98389642 0.01872322 -0.03839118 -0.09592923 -0.10702297 -0.09729877] [ 0.01872322 0.92317564 -0.00126495 0.34627269 -0.09792622 0.13379184] [-0.03839118 -0.00126495 0.85968895 -0.09412702 -0.4916874 -0.09403736] [ 0.09592923 -0.34627269 0.09412702 0.92774284 -0.01313115 -0.03396633] [ 0.10702297 0.09792622 0.4916874 -0.01313115 0.85816974 -0.02392281] [ 0.09729877 -0.13379184 0.09403736 -0.03396633 -0.02392281 0.98084844]] Current Energy: -2.855639168402048 true energy -2.855762215867439 dvec [(np.complex128(0.13311560013264928+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.1360327781797804+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.09172718677890154+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.2518796049075652+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.12612950639436693+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.1960191753350156+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.16888968342063598+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.18595207614225323+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.18779023164462422+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.05634153373199127 ITERATION NUMBER : 2 unitary [[ 0.98876823 0.01628796 -0.02189467 -0.08831305 -0.08139045 -0.08467065] [ 0.0224637 0.91787913 0.00754041 0.35705807 -0.08683799 0.14800378] [-0.03345247 -0.00689636 0.87261581 -0.08249537 -0.47415714 -0.07579267] [ 0.08711517 -0.35779724 0.08259369 0.9254254 -0.00455821 -0.03372571] [ 0.07790186 0.08528312 0.47453161 -0.01319162 0.87226738 -0.02129404] [ 0.08399973 -0.14796272 0.07748189 -0.0363135 -0.0117726 0.98162639]] Current Energy: -2.8798197509192507 true energy -2.880729115492276 dvec [(np.complex128(0.12586324237597135+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.11635338963574188+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.07214209682833139+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.16712654806439728+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.11181163224587773+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.12626770025249584+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.13945142621375045+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.15298312961105048+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.14091964239206287+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.06594481478288675 ITERATION NUMBER : 3 unitary [[ 9.92894545e-01 1.14115660e-02 -5.87521191e-03 -7.70186576e-02 -5.51116524e-02 -7.08979024e-02] [ 2.60516417e-02 9.10753895e-01 1.73230889e-02 3.70475840e-01 -7.29440787e-02 1.64241829e-01] [-2.93499492e-02 -1.41784574e-02 8.84603346e-01 -6.93077059e-02 -4.56535391e-01 -5.64477738e-02] [ 7.40387291e-02 -3.71977900e-01 6.90238267e-02 9.22063824e-01 4.77026067e-03 -3.40876736e-02] [ 4.84182317e-02 7.05194462e-02 4.57011577e-01 -1.49718333e-02 8.84982755e-01 -2.01113972e-02] [ 6.92405679e-02 -1.63876598e-01 5.93164601e-02 -3.98292586e-02 2.68590837e-04 9.81450620e-01]] Current Energy: -2.901581571777177 true energy -2.90172017668864 dvec [(np.complex128(0.09803486708515219+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.08042887968230017+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.051428336695724226+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.07400812547980172+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.09244923128080866+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.06976005520858272+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.10524245692499902+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.10778058433247523+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.08817249266541517+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.07145479600551409 ITERATION NUMBER : 4 unitary [[ 0.99630268 0.00242784 0.00968296 -0.06033137 -0.02805891 -0.05342421] [ 0.02944622 0.90032868 0.02949591 0.38816808 -0.05302032 0.18489341] [-0.0260764 -0.02426822 0.89565322 -0.05334473 -0.43875792 -0.0343833 ] [ 0.05448169 -0.39049166 0.05174116 0.91671533 0.01531824 -0.03562615] [ 0.01850391 0.05079352 0.4390193 -0.02004433 0.89637536 -0.02119237] [ 0.05023216 -0.18371095 0.03776834 -0.04551092 0.0130229 0.97982638]] Current Energy: -2.9156074784816735 true energy -2.915731463597599 dvec [(np.complex128(0.06690604735308885+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.04468374649675236+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.04357005485060929+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.002137226683705999+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.05897107441788871+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.024652711044558323+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.05877250138680977+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.058488591110638935+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.03903896375680379+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.06456329359242352 ITERATION NUMBER : 5 unitary [[ 0.99841438 -0.01137027 0.02042842 -0.0391043 -0.00805903 -0.03206276] [ 0.03166751 0.88690889 0.04407489 0.40783329 -0.0250033 0.20855223] [-0.02409595 -0.03715599 0.90465119 -0.03465197 -0.42224539 -0.01237417] [ 0.02928689 -0.41093132 0.03047213 0.90948372 0.02627169 -0.03870838] [-0.0030564 0.02460156 0.42200764 -0.030176 0.90538354 -0.02578799] [ 0.0267994 -0.20594413 0.01507696 -0.05358053 0.02468106 0.97629989]] Current Energy: -2.9220270508854678 true energy -2.9221347356715905 dvec [(np.complex128(0.030078246187414337+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.01954256838651816+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.025758019128118523+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(-0.014000002988387373+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.03608033428599095+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.003021308972332798+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.020985386703569125+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.008783826642579193+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.01298084260018445+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.032011989102227904 ITERATION NUMBER : 6 unitary [[ 0.99917054 -0.02688083 0.02138952 -0.01605596 -0.00577386 -0.01367536] [ 0.0322495 0.87378184 0.0570777 0.42437187 0.00352998 0.22826182] [-0.02338923 -0.05298923 0.90916147 -0.00899265 -0.4122936 0.00190173] [ 0.00260167 -0.42744476 0.00189221 0.90218999 0.03908756 -0.04249709] [-0.00472279 -0.0013726 0.41195291 -0.04243076 0.90963115 -0.03227094] [ 0.0064867 -0.22419623 -0.00112197 -0.06182801 0.03180442 0.97203832]] Current Energy: -2.923571899134087 true energy -2.9235351521017345 dvec [(np.complex128(0.00874646936866534+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.0003159578405415031+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.012816300947431048+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(-0.011203219546101848+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.013618842223797658+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.009913148190446058+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.014314008902573054+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(-0.0032655133889614996+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.014007759391965212+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.015449735839785013 ITERATION NUMBER : 7 unitary [[ 9.99162534e-01 -3.36512944e-02 1.87942515e-02 -5.33473464e-03 -1.05293953e-02 -7.01917187e-03] [ 3.21910898e-02 8.68850395e-01 6.46331974e-02 4.31652705e-01 2.09278808e-02 2.30484794e-01] [-2.34361575e-02 -6.18951454e-02 9.09496255e-01 6.67251701e-03 -4.10307108e-01 6.31301666e-03] [-9.36444927e-03 -4.34138698e-01 -1.51316840e-02 8.98368793e-01 4.64074902e-02 -4.45733942e-02] [ 7.56353101e-04 -1.76671652e-02 4.09898082e-01 -5.04409358e-02 9.09828133e-01 -3.65970188e-02] [-6.67170093e-04 -2.26598840e-01 -6.36262013e-03 -6.31837387e-02 3.40344732e-02 9.71319467e-01]] Current Energy: -2.9239362384154335 true energy -2.9238837162583105 dvec [(np.complex128(0.0017946104559911037+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.005167327165156221+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.006647390881771056+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.002216458028389035+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.010369303025167111+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.0012919023864796653+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.004090435384382255+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.0054599966493354135+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.003776586592693803+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.008149848130573161 ITERATION NUMBER : 8 unitary [[ 0.99909407 -0.03618009 0.01671244 -0.00223208 -0.01458408 -0.00224976] [ 0.03221502 0.86892288 0.06751216 0.43150209 0.0272969 0.22899376] [-0.02354062 -0.06716718 0.91081148 0.01415406 -0.40623443 0.01140659] [-0.01267267 -0.43356976 -0.02335305 0.89822349 0.05010338 -0.04467122] [ 0.00544313 -0.02370559 0.40608408 -0.05353502 0.91113863 -0.03826925] [-0.00537125 -0.224962 -0.01164515 -0.06268326 0.03649407 0.97157945]] Current Energy: -2.923988269625067 true energy -2.9239876687572366 dvec [(np.complex128(0.006066934744438236+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(-0.003724313067892976+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.002909016113757866+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(-0.001992129690603965+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.0038444887033365514+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(0.002820434504725966+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.001443130170217812+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(6.482498564203132e-05+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.010311145573541998+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.0061199528794130265 ITERATION NUMBER : 9 unitary [[ 9.99080850e-01 -3.68341840e-02 1.70655469e-02 -1.72625267e-03 -1.36222455e-02 -9.59290810e-04] [ 3.21961675e-02 8.67237489e-01 6.95875299e-02 4.33293307e-01 3.23618645e-02 2.30715713e-01] [-2.36078956e-02 -6.95406192e-02 9.10873348e-01 1.81785328e-02 -4.05493414e-01 1.26943055e-02] [-1.33629417e-02 -4.35370157e-01 -2.77452217e-02 8.97082884e-01 5.19162168e-02 -4.52931291e-02] [ 4.32501262e-03 -2.82688787e-02 4.05254451e-01 -5.58482451e-02 9.11192467e-01 -3.95000841e-02] [-6.80116730e-03 -2.26627845e-01 -1.32332585e-02 -6.36140278e-02 3.70840960e-02 9.71080053e-01]] Current Energy: -2.9240271927265646 true energy -2.924023588452438 dvec [(np.complex128(-0.003031542241707406+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(0.0018242445978919608+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.006610909807702604+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.0016093083470417116+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.0020197901109114628+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(-0.0010336703186756835+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(0.006027738791639956+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.0018324042356210601+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(-0.0013914950230603743+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.005498385049381881 ITERATION NUMBER : 10 unitary [[ 9.99037906e-01 -3.79802300e-02 1.66404748e-02 4.78901103e-04 -1.42590150e-02 -5.56151717e-04] [ 3.22313556e-02 8.67950850e-01 7.04409111e-02 4.31575652e-01 3.40765429e-02 2.30741815e-01] [-2.36621276e-02 -7.14188000e-02 9.11184569e-01 1.96710298e-02 -4.04248098e-01 1.66932880e-02] [-1.56932451e-02 -4.33584658e-01 -2.95125632e-02 8.97819039e-01 5.28323857e-02 -4.49086523e-02] [ 5.14501755e-03 -2.99459912e-02 4.04153103e-01 -5.67266481e-02 9.11548791e-01 -3.99740571e-02] [-7.19414442e-03 -2.26331087e-01 -1.71211105e-02 -6.37050838e-02 3.88134715e-02 9.71012115e-01]] Current Energy: -2.9240302348937317 true energy -2.9240437513503688 dvec [(np.complex128(0.00794614163307366+0j), -1.0 [0^ 6] + -1.0 [1^ 7] + 1.0 [6^ 0] + 1.0 [7^ 1]), (np.complex128(-0.0025293422026237133+0j), -1.0 [2^ 6] + -1.0 [3^ 7] + 1.0 [6^ 2] + 1.0 [7^ 3]), (np.complex128(0.000470043051522625+0j), -1.0 [4^ 6] + -1.0 [5^ 7] + 1.0 [6^ 4] + 1.0 [7^ 5]), (np.complex128(0.001262778585715399+0j), -1.0 [0^ 8] + -1.0 [1^ 9] + 1.0 [8^ 0] + 1.0 [9^ 1]), (np.complex128(0.00255958910826229+0j), -1.0 [2^ 8] + -1.0 [3^ 9] + 1.0 [8^ 2] + 1.0 [9^ 3]), (np.complex128(-0.0007140534985449476+0j), -1.0 [4^ 8] + -1.0 [5^ 9] + 1.0 [8^ 4] + 1.0 [9^ 5]), (np.complex128(-0.005101986643072931+0j), -1.0 [0^ 10] + -1.0 [1^ 11] + 1.0 [10^ 0] + 1.0 [11^ 1]), (np.complex128(0.0022685510894237537+0j), -1.0 [2^ 10] + -1.0 [3^ 11] + 1.0 [10^ 2] + 1.0 [11^ 3]), (np.complex128(0.005006563852632914+0j), -1.0 [4^ 10] + -1.0 [5^ 11] + 1.0 [10^ 4] + 1.0 [11^ 5])] New fr values norm 0.004685693747951088 Finished Optimization
Each iteration prints out a variety of information that the user might find useful. Watching energies go down is known to be one of the best forms of entertainment during a shelter-in-place order.
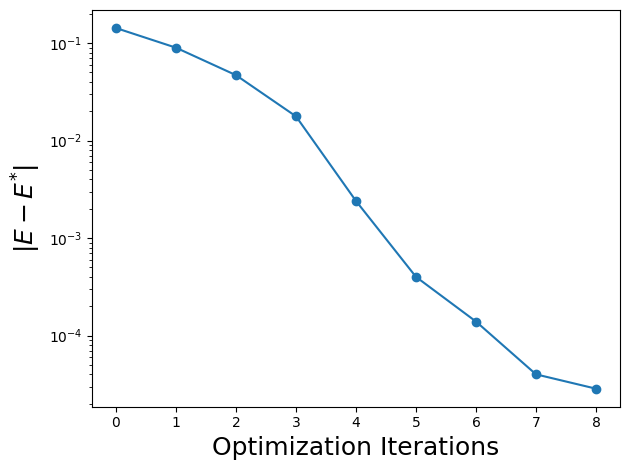
After the optimization we can print the energy as a function of iteration number to see close the energy gets to the true minium.
import matplotlib.pyplot as plt
plt.semilogy(range(len(result.func_vals)),
np.abs(np.array(result.func_vals) - energy(parameters)),
'C0o-')
plt.xlabel("Optimization Iterations", fontsize=18)
plt.ylabel(r"$|E - E^{*}|$", fontsize=18)
plt.tight_layout()
plt.show()