 View on QuantumAI
|
 Run in Google Colab
|
 View source on GitHub
|
 Download notebook
|
Wrap tket's compilation unit framework to keep track of qubit mappings and work with generic devices.
Setup
Install the ReCirq package:
try:
import recirq
except ImportError:
!pip install -q git+https://github.com/quantumlib/ReCirq sympy~=1.6
Now import Cirq, ReCirq and the module dependencies:
import cirq
import recirq
import networkx as nx
from cirq.contrib.svg import SVGCircuit
import numpy as np
from pytket.predicates import CompilationUnit, ConnectivityPredicate
from pytket.passes import SequencePass, RoutingPass, DecomposeSwapsToCXs
from pytket.placement import GraphPlacement
Example circuit
We'll route a 3-regular circuit to Sycamore23. To try to clear up some of the confusion about which indices are which, we'll construct the initial circuit with LineQubits 10 through 19 which should be thought of as "logical indices".
from recirq.qaoa.problem_circuits import get_generic_qaoa_circuit
from recirq.qaoa.gates_and_compilation import compile_problem_unitary_to_arbitrary_zz, \
compile_driver_unitary_to_rx
problem_graph = nx.random_regular_graph(d=3, n=10)
nx.set_edge_attributes(problem_graph, values=1, name='weight')
circuit_qubits = cirq.LineQubit.range(10, 20)
gammas = np.random.randn(2)
betas = np.random.randn(2)
circuit = get_generic_qaoa_circuit(
problem_graph=problem_graph,
qubits=circuit_qubits,
gammas=gammas,
betas=betas)
circuit = compile_problem_unitary_to_arbitrary_zz(circuit)
circuit = compile_driver_unitary_to_rx(circuit)
SVGCircuit(circuit)
findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found.
"Route" this circuit
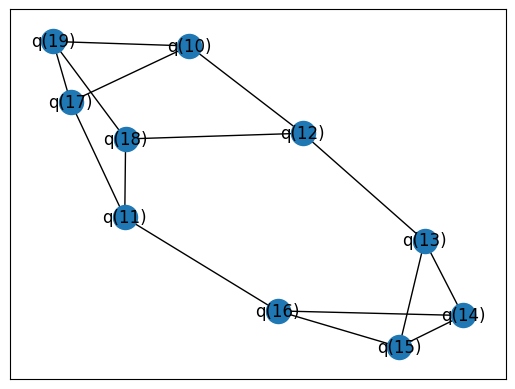
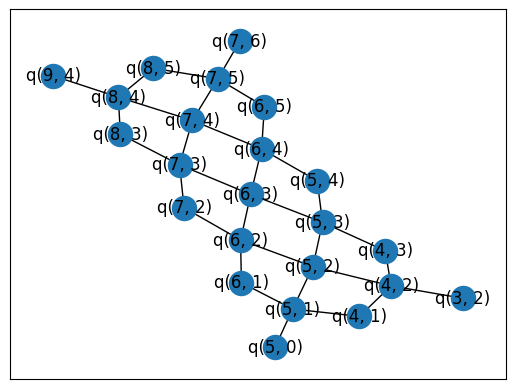
Let's look at the "connectivity graph" of the circuit vs. that of the device
import cirq.contrib.routing as ccr
uncompiled_c_graph = ccr.get_circuit_connectivity(circuit)
nx.draw_networkx(uncompiled_c_graph)
import cirq_google as cg
dev_graph = ccr.gridqubits_to_graph_device(cg.Sycamore23.metadata.qubit_set)
nx.draw_networkx(dev_graph)
# alias for the device. If this notebook were wrapped
# in a function, `circuit` and `device` would be the arguments
device = cg.Sycamore23
Convert to pytket Device
The provided function doesn't work with GridDevice. We use existing functionality to turn Devices into graphs to provide a more robust solution.
import pytket
from recirq.qaoa.placement import _device_to_tket_device
tk_circuit = pytket.extensions.cirq.cirq_to_tk(circuit)
tk_device = _device_to_tket_device(device)
tk_circuit.qubits
[q[10], q[11], q[12], q[13], q[14], q[15], q[16], q[17], q[18], q[19]]
tk_device.coupling
[(grid[8, 5], grid[7, 5]), (grid[8, 5], grid[8, 4]), (grid[7, 5], grid[7, 4]), (grid[7, 5], grid[6, 5]), (grid[7, 5], grid[7, 6]), (grid[8, 4], grid[9, 4]), (grid[8, 4], grid[7, 4]), (grid[8, 4], grid[8, 3]), (grid[7, 3], grid[7, 2]), (grid[7, 3], grid[6, 3]), (grid[7, 3], grid[7, 4]), (grid[7, 3], grid[8, 3]), (grid[7, 2], grid[6, 2]), (grid[6, 3], grid[6, 4]), (grid[6, 3], grid[5, 3]), (grid[6, 3], grid[6, 2]), (grid[7, 4], grid[6, 4]), (grid[5, 0], grid[5, 1]), (grid[5, 1], grid[5, 2]), (grid[5, 1], grid[6, 1]), (grid[5, 1], grid[4, 1]), (grid[6, 4], grid[6, 5]), (grid[6, 4], grid[5, 4]), (grid[5, 4], grid[5, 3]), (grid[5, 2], grid[5, 3]), (grid[5, 2], grid[4, 2]), (grid[5, 2], grid[6, 2]), (grid[5, 3], grid[4, 3]), (grid[4, 2], grid[4, 1]), (grid[4, 2], grid[3, 2]), (grid[4, 2], grid[4, 3]), (grid[6, 2], grid[6, 1])]
Placement and routing pass
from pytket.predicates import CompilationUnit, ConnectivityPredicate
from pytket.passes import SequencePass, RoutingPass, DecomposeSwapsToCXs, PlacementPass
from pytket.placement import GraphPlacement
unit = CompilationUnit(tk_circuit, [ConnectivityPredicate(tk_device)])
passes = SequencePass([
PlacementPass(GraphPlacement(tk_device)),
RoutingPass(tk_device)])
passes.apply(unit)
valid = unit.check_all_predicates()
assert valid
The initial mapping
This maps from logical LineQubits to "physical" GridQubits
unit.initial_map
{q[10]: grid[5, 4],
q[11]: grid[6, 2],
q[12]: grid[6, 4],
q[13]: grid[7, 4],
q[14]: grid[7, 3],
q[15]: grid[8, 3],
q[16]: grid[7, 2],
q[17]: grid[5, 2],
q[18]: grid[6, 3],
q[19]: grid[5, 3]}
Bookkept initial mapping
We "decode" our tket conventions back into Cirq idioms.
def tk_to_cirq_qubit(tk):
ind = tk.index
return cirq.LineQubit(ind[0]) if len(ind) == 1 else cirq.GridQubit(*ind)
initial_map = {tk_to_cirq_qubit(n1): tk_to_cirq_qubit(n2) for n1, n2 in unit.initial_map.items()}
initial_map
{cirq.LineQubit(10): cirq.GridQubit(5, 4),
cirq.LineQubit(11): cirq.GridQubit(6, 2),
cirq.LineQubit(12): cirq.GridQubit(6, 4),
cirq.LineQubit(13): cirq.GridQubit(7, 4),
cirq.LineQubit(14): cirq.GridQubit(7, 3),
cirq.LineQubit(15): cirq.GridQubit(8, 3),
cirq.LineQubit(16): cirq.GridQubit(7, 2),
cirq.LineQubit(17): cirq.GridQubit(5, 2),
cirq.LineQubit(18): cirq.GridQubit(6, 3),
cirq.LineQubit(19): cirq.GridQubit(5, 3)}
The final mapping
This maps from logical LineQubits to final GridQubits
unit.final_map
{q[10]: grid[5, 4],
q[11]: grid[6, 2],
q[12]: grid[6, 4],
q[13]: grid[7, 4],
q[14]: grid[8, 3],
q[15]: grid[7, 3],
q[16]: grid[7, 2],
q[17]: grid[5, 2],
q[18]: grid[6, 3],
q[19]: grid[5, 3]}
final_map = {tk_to_cirq_qubit(n1): tk_to_cirq_qubit(n2)
for n1, n2 in unit.final_map.items()}
final_map
{cirq.LineQubit(10): cirq.GridQubit(5, 4),
cirq.LineQubit(11): cirq.GridQubit(6, 2),
cirq.LineQubit(12): cirq.GridQubit(6, 4),
cirq.LineQubit(13): cirq.GridQubit(7, 4),
cirq.LineQubit(14): cirq.GridQubit(8, 3),
cirq.LineQubit(15): cirq.GridQubit(7, 3),
cirq.LineQubit(16): cirq.GridQubit(7, 2),
cirq.LineQubit(17): cirq.GridQubit(5, 2),
cirq.LineQubit(18): cirq.GridQubit(6, 3),
cirq.LineQubit(19): cirq.GridQubit(5, 3)}
The compilation unit applies the mapping
So our circuit qubits are now GridQubits
unit.circuit.qubits
[grid[5, 2], grid[5, 3], grid[5, 4], grid[6, 2], grid[6, 3], grid[6, 4], grid[7, 2], grid[7, 3], grid[7, 4], grid[8, 3]]
Convert the circuit back to Cirq
routed_circuit = pytket.extensions.cirq.tk_to_cirq(unit.circuit)
SVGCircuit(routed_circuit)
findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found.
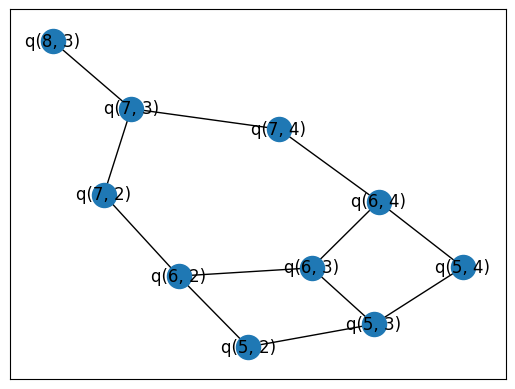
Now it's nice and compiled
routed_c_graph = ccr.get_circuit_connectivity(routed_circuit)
nx.draw_networkx(routed_c_graph)
Check that circuits are equivalent
for op in routed_circuit.all_operations():
if len(op.qubits) != 2:
continue
a, b = op.qubits
assert a.is_adjacent(b)
import cirq.contrib.acquaintance as cca
def permute_gate(qubits, permutation):
return cca.LinearPermutationGate(
num_qubits=len(qubits),
permutation={i: permutation[i] for i in range(len(permutation))}
).on(*qubits)
final_to_initial_map = {final_map[cq]: initial_map[cq]
for cq in circuit_qubits}
initial_qubits = [initial_map[cq] for cq in circuit_qubits]
final_permutation = [initial_qubits.index(final_to_initial_map[q])
for q in initial_qubits]
rcircuit_with_perm = routed_circuit.copy()
rcircuit_with_perm.append(permute_gate(initial_qubits, final_permutation))
expected = circuit.unitary(qubit_order=cirq.QubitOrder.explicit(circuit_qubits))
actual = rcircuit_with_perm.unitary(qubit_order=cirq.QubitOrder.explicit(initial_qubits))
cirq.testing.assert_allclose_up_to_global_phase(expected, actual, atol=1e-8)